El número aureo o de oro (también llamado número dorado, sección áurea, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) representado por la letra griega φ (fi) (en honor al escultor griego Fidias), es el número irracional:
Una sección áurea es una división en dos de un segmento según proporciones dadas por el número áureo. La longitud total a+b es al segmento más largo a como a es al segmento más cortob.
Se trata de un número algebraico que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza en elementos tales como caracolas, nervaduras de las hojas de algunos árboles, el grosor de las ramas, etc.
Así mismo, se atribuye un carácter estético especial a los objetos que siguen la razón áurea, así como una importancia mística. A lo largo de la historia, se le ha atribuido importancia en diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido objetables para las matemáticas y la arqueología.
El número phi en la arquitectura.
 Es incontable la cantidad de obras arquitectónicas de todops los tiempos en los que se hace presente el número de Oro. En La Gran Pirámide de Keops, el cociente entre la altura de uno de los tres triángulos que forman la pirámide y el lado es 2Φ. La pirámide de Keops mide 230 metros de lado, la base de la pirámide es cuadrada.
Es incontable la cantidad de obras arquitectónicas de todops los tiempos en los que se hace presente el número de Oro. En La Gran Pirámide de Keops, el cociente entre la altura de uno de los tres triángulos que forman la pirámide y el lado es 2Φ. La pirámide de Keops mide 230 metros de lado, la base de la pirámide es cuadrada.
AC = 230/2 = 115
√Φ ≈ 1.272
AB = √Φ –> √Φ x 115 ≈ 146,28 que son los metros de altura de la pirámide de Keops.
BC = Φ x 115 ≈ 186,07 metros desde el centro de un lado de la base hasta el pico de la pirámide.
 Los ejes de sus cuatro pilares forman un cuadrado de 100 metros, que seria el lado pequeño de un rectángulo áureo. Pues poniendo dos rectángulos conseguimos la altura de esta torre. 100 x Φ x 2 ≈ 323,61 metros que es la altura de la torre.
Los ejes de sus cuatro pilares forman un cuadrado de 100 metros, que seria el lado pequeño de un rectángulo áureo. Pues poniendo dos rectángulos conseguimos la altura de esta torre. 100 x Φ x 2 ≈ 323,61 metros que es la altura de la torre.
También se encuentra en las diferentes partes de la torre, vea el dibujo donde el espacio azul seria igual a uno y Phi seria el espacio azul más el dorado.
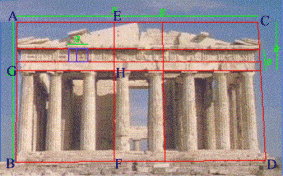
El creador del Partenón (Debajo) fue Phidias. En realidad, el número de oro se llama Phi en su nombre, y la abreviatura Ø corresponde a la inicial de Phidias en griego.
La fachada del partenón es un perfecto rectángulo de oro, pero además, hay otra serie de medidas en el edificio que también poseen proporciones áureas:
En la foto están marc ados los rectángulos áureos: ABCD, AEGH, AEBF, y sus simétricos. Además, la zona de las molduras (en color violeta) también está compuesta por rectángulos áureos.
La razón áurea y el Arte.
 El rosotro de la Gioconda, pintada por Leonardo, se encuadra en un rectángulo áureo. [Razón áurea en la Gioconda]
El rosotro de la Gioconda, pintada por Leonardo, se encuadra en un rectángulo áureo. [Razón áurea en la Gioconda]
Unas proporciones armoniosas para el cuerpo, que estudiaron antes los griegos y romanos, las plasmó en este dibujo Leonardo da Vinci. Sirvió para ilustrar el libro La Divina Proporción de Luca Pacioli editado en 1509.
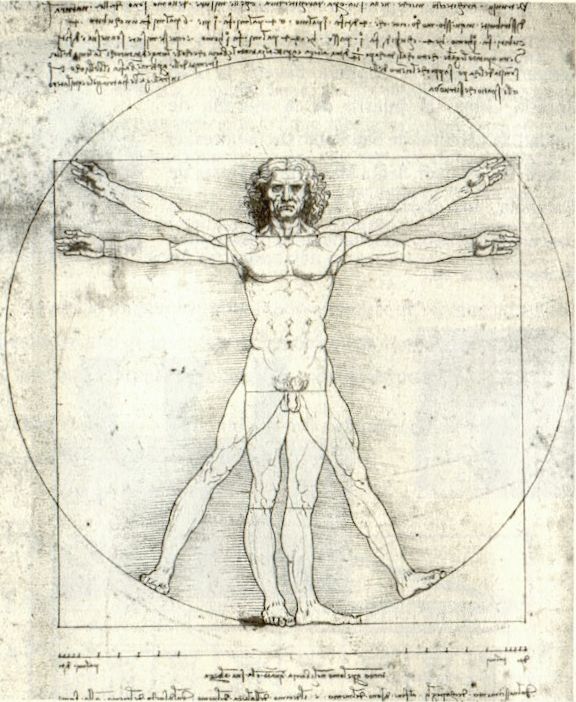 En dicho libro se describen cuales han de ser las proporciones de las construcciones artísticas. En particular, Pacioli propone un hombre perfecto en el que las relaciones entre las distintas partes de su cuerpo sean proporciones áureas. Estirando manos y pies y haciendo centro en el ombligo se dibuja la circunferencia. El cuadrado tiene por lado la altura del cuerpo que coincide, en un cuerpo armonioso, con la longitud entre los extremos de los dedos de ambas manos cuando los brazos están extendidos y formando un ángulo de 90º con el tronco. Resulta que el cociente entre la altura del hombre (lado del cuadrado) y la distancia del ombligo a la punta de la mano (radio de la circunferencia) es el número áureo.
En dicho libro se describen cuales han de ser las proporciones de las construcciones artísticas. En particular, Pacioli propone un hombre perfecto en el que las relaciones entre las distintas partes de su cuerpo sean proporciones áureas. Estirando manos y pies y haciendo centro en el ombligo se dibuja la circunferencia. El cuadrado tiene por lado la altura del cuerpo que coincide, en un cuerpo armonioso, con la longitud entre los extremos de los dedos de ambas manos cuando los brazos están extendidos y formando un ángulo de 90º con el tronco. Resulta que el cociente entre la altura del hombre (lado del cuadrado) y la distancia del ombligo a la punta de la mano (radio de la circunferencia) es el número áureo.
Phi en la música.
En varias sonatas para piano de Mozart, la proporción entre el desarrollo del tema y su introducción es la más cercana posible a la razón áurea.
Caracteristicas de la Sonata Nº1 para piano de Mozart:
- El segundo tema armónico de la obra siempre es más extenso que el primero
- Primer movimiento subdividido en 38 y 62 compases y 63 / 38 = 1.6315
- Segundo movimiento subdividido en 28 y 46 compases y 46 / 28 = 1.6428
Aunque no sabemos con precisión que Beethoven estuviera al tanto de ésto, pero en su Quinta Sinfonía, distribuye el tema siguiendo la sección áurea. El clímax de la obra se encuentra al 61,8 % de ella.
Los músicos de jazz autodidactas pueden no ser conscientes de la teoría de escalas, armonía y formas que usan habitualmente, pero igual producen obras armoniosas.
El Piano:El piano está constituido por siete octavas ordenadas de forma creciente de graves a agudas.
Así, los primeros seis números de la Sucesión de Fibonacci figuran en una octava de piano, la cual consiste en 13 teclas, 8 teclas blancas y 5 teclas negras ( en grupos de 2 y 3).
La Razón Aurea en la Naturaleza.
Podemos establecer una relación con Phi en la distancia de los diferentes planetas del sistema solar al sol, en las semillas del girasol, en las proporciones morfológicas de una abeja, en la temperatura corporal de los animales y en una infinidad de fenómenos naturales. A continuación y por cuestiones de espacio, solo detallaremos una de éstas relaciones del número de oro con la naturaleza.
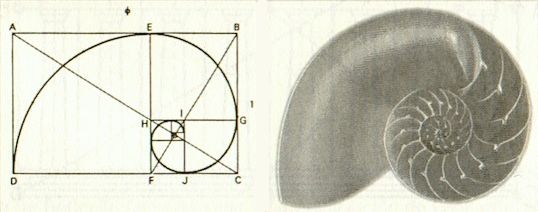
La imágen anterios es unaconcha de Nautilo. Si del rectángulo áureo ABCD extraemos el cuadrado AEFD nos queda otro rectángulo áureo EBCF, a este le extraemos el cuadrado EBHG tenemos otro rectángulo áureo GHCF y así podríamos seguir hasta el infinito.
Si a partir de estos cuadrados resultantes trazamos una curva que empieza por D hasta E con centro F después de E con centro G hasta H, aquí también podríamos seguir hasta el infinito, conseguimos una espiral logarítmica que se puede encontrar en la naturaleza en plantas y en animales, como en la concha de los nautilos.
El núero de Phidias en la vida cotidiana. La Razón Aurea.
El número áureo no solo lo podemos encontrar en la naturaleza o en las antiguas construcciones y representaciones artísticas, diariamente manejamos objetos en los cuales se ha tenido en cuenta las proporciones áureas para su elaboración. Por ejemplo, la mayoría de las tarjetas de crédito así como nuestro carnet tienen la proporción de un rectángulo áureo. También lo podemos encontrar en las cajetillas de tabaco, construcción de muebles, marcos para ventanas, camas, etc.